My current Year Nine Maths class (MAT091A) must be like many around Australia. It’s very mixed. It has all sorts of critters in residence. Some of its students always find it easy to learn mathematics, are cognitively engaged and self-motivated. Others might be school-refuser’s, have personal disorders such as anxiety, or low literacy attainment. For some, the home environment is dysfunctional. A mathematics teacher’s role here is complex and full of challenges.
MAT091A marks the first case where I’ve flipped a class below Year 10 level, and the first time I’ve used this meta-strategy with a “challenging” class. We are fortunate to have 280 minutes per week contact time, so I’ve been able to implement several flipped learning strategies already in this class with its aforementioned characteristics and its absence of any prior student experience with flipped learning. The Good Stuff has been happening: my videos are watched, and if not, the in-flip is used. Flipped Mastery has been the staple, where I speak with every student, every lesson. Even though students have at times resisted flipping, the implementation is still progressing, as it should. There is much more work to do, however.
I have noticed, unsurprisingly, that there are substantial issues, to do with MAT091A student dispositions and skills in solving problems. I have thought that it would be great to be able to use the freed-up time due to flipping my videos to improve on the status quo. Problem solving is an immensely important element of a mathematics education, and in the twenty-first century, it is cited increasingly as a vital skill.
Problem Solving Teaching – A Background Narrative
My focus on student problem solving first started in a highly resolute manner back in 2006 when I first became a Mathematics HoD. I was concerned about senior student performance initially in the Modelling and Problem Solving criterion of the Queensland Senior Mathematics subjects. However, since then my interest has deepened, and I am active in teaching problem solving at all high school year levels, as an element of both Mathematics, the subject, and numeracy, the cross-curricula ability. One of the key junctures was as a HoD in 2013, when every faculty in my school had to action a mandate from the leadership team to implement Reciprocal Teaching authentically in their subject areas. Darn! As far as I was aware, no maths person was crazy enough to even try this. This mandate forced me to find a way to blend the Great Stuff: Problem-Solving Teaching (PST) – was not going to dump this! – with Reciprocal Teaching (RT) – what the English teachers did. Whilst I value RT and had used RT when teaching English myself, I was at a loss to find how in the world to make these two great strategies work as one machine. So, I used a truly unique plan one Sunday morning. Google.
My Google search of “Problem Solving Teaching + Reciprocal Teaching” yielded an immediate bulls-eye. Unbelievably, the first result listed was an article about RT in Maths, written by Yvonne Reilly, Jodie Parsons and Elizabeth Bortolot of Sunshine College, Victoria. This was Great Stuff! Later a team from my school comprising of the principal, three deputies and three HoD went on an expedition to some of the best schools we could find in Victoria. Sunshine College was one of these. We saw the aforementioned authors in action in their classrooms. This school seemed to have every excuse not to be producing great outcomes, with well over fifty different languages spoken in students’ homes, and an ICSEA index of well below 1000. However, the opposite was true. What the staff were doing there was amazingly successful – especially with regard to problem solving in Maths classes.
Reciprocal Teaching in Hattie’s Visible Learning, has a high effect size of d = 0.74. It is a renowned strategy for reading comprehension, and it is a collaborative group process.
- Predicting
- Clarifying
- Questioning
- Summarising
However, the key change Reilly et al made, and thus, my way of meshing PST and RT, involved replacing Questioning, which usually has little relevance in a high school mathematical problem-solving context. Questioning in RT is where students textually analyse, and interrogate an extended text and explore deeper meanings. The vital change was to use Solving instead:
- Predicting
- Clarifying
- Solving
- Summarising
This key change, plus refining the nature of the other three steps to suit a high school Maths context was what we needed. Now for the job of making it our own.
As a fan of PST (d = 0.61), and in particular the heuristic work of George Pólya, I set to work on modifying the ideas from Sunshine College for our needs. Over four years and a few iterations in collaboration with staff (past and present) from my current school, we have arrived at the following process (see Figure 1) which we call Reciprocal Maths Teaching (RMT), or just Reciprocal Maths. RMT dovetails Pólya’s PST steps with a reading comprehension strategy, in a collaborative context. Pólya’s steps are inherent in RMT.
Pólya’s steps:
- Understand the problem
- Devise a plan.
- Carry out the plan.
- Look back.
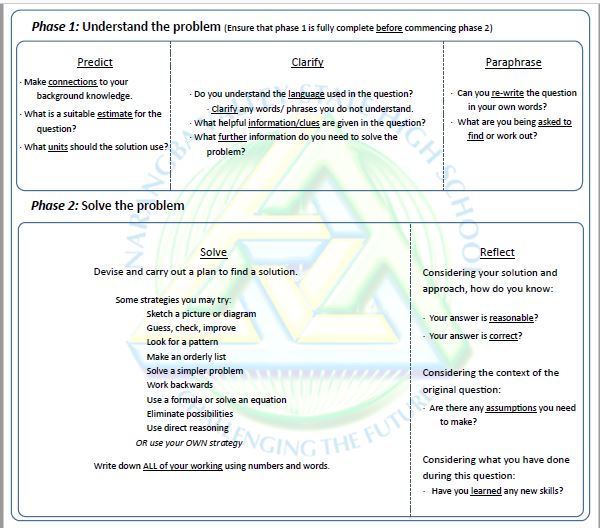
By explicitly teaching students these RMT steps, as well as the “toolkit” of mathematical strategies in Solve, students gradually build an arsenal of tactics to tackle problems they may encounter in future. Our Maths faculty has spent up on physical resources to facilitate the implementation of RMT. Students from Years Seven to Nine have a trolley in their Maths classroom with laser-etched, ceramic-coated, tablet-sized whiteboards. On one side is a blank template version of Figure 1, where students may write their responses with whiteboard markers, and the other side is blank for rough working, of a temporary nature. We found from Sunshine College that mini-whiteboards give some students more courage to take a risk and have a go at the problem. We supply the stationery too. Additionally, we have a truly gigantic outdoor RMT template (as per Figure 1) with three RMT template full-size whiteboards.
Flipped RMT – Observations Thus Far
I’ve been using RMT since 2013, and I knew that this would never be an easy quick fix in MAT091A. And it hasn’t been! Just like when a teacher trains a new class over weeks in how to watch flipped videos, take Cornell Notes, and use the Group Space responsibly, Flipped RMT is a lot of work initially. Certainly, by flipping MAT091A, I have far more contact time available than traditional non-flipped Maths classes to train students.
Group norms comprise an essential set of skills and protocols that students must be trained in. In MAT091A some students take over, others avoid the tasks at hand, some disrupt other groups because they don’t like the group I’ve put them in, and some initially refuse as they still haven’t decided that problem solving is worth the effort. However, collaborative skills are essential twenty-first century skills. Students learn by hearing their peers explain mathematical concepts or strategies, and deep learning occurs when students teach other students.
Some students often like to immediately go to the Solve step (I’m looking at you boys!). After all it’s the answer that matters – nothing else, right? My students sometimes come from households where parents can be heard to say (e.g. at PT interviews) that “It’s maths. It’s only right or wrong…”. Whether we flip or not, teachers must be patient and never give in to students who balk at the other key stages Predict, Clarify and Reflect.
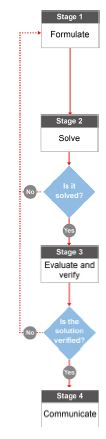
I note with great interest that the new SATE system in Queensland (the new senior schooling system for curriculum, assessment and tertiary entrance – the largest systemic change in decades) for Senior Mathematics will assess students against a process and rubrics which are remarkably consistent with our RMT modus operandi. See Figure 2. Hence, in terms of preparing students for the increased rigour and required levels of initiative and insight, we think we are on the right track.
The amount of active learning has been great to watch during RMT sessions. It is also often the reason why some students initially resist. Groups are typically small (I like two or three), and provided the right questions are provided (we have a growing bank of problems that our numeracy coach has been assembling), students wrestle with collective reasoning, apply their mathematical concepts and strategies in partnerships, and justify the reasonableness (or not!) of their results. Higher order thinking is required, as are initiative and insight. Sometimes, we can get students to re-watch an Individual Space video if no students in the group can recall the maths underlying the problem. This is sometimes, my job as a facilitator – to intervene and diagnose “just in time”, what the blockers might be. Other times, I like to just fire questions at students to prompt them, in little ways. The thinking needs to come from the students, wherever possible. As a result, I get to speak to lots of my students and have substantive conversations about the maths during RMT. It certainly does not do working relationships any harm.
Flipped RMT – What Next?
I am very confident in the validity and effectiveness of this strategy. However, it is crucial that I do some formal diagnostic work to more scientifically measure the effect of RMT in MAT091A. This will be a future focus. Additionally, I’m still not quite satisfied with some of the finer elements in our RMT process. For example, I want to “beef up” Predict, as students demonstrate some uncertainty around how to respond to this phase. We need to provide training that is more meaningful to students to help them understand and value this part of the process.
Note that we don’t use the same collaboration dynamic as English classes often use with RT. In English classes four students each take, or are assigned, one role: Predictor, Clarifier, Questioner, or Summariser. We have not pursued this dynamic in RMT, as we value that each student is participating in every step. However, perhaps I should do more investigation regarding these mechanics. At this stage, I’m interested in mimicking the “one role” mode from RT and using a system of rotation, so that students become experienced in all processes. No doubt, what I find will be interesting.
Finally, I’m beginning my journey in gamifying RMT. I’m calling the groups “tribes” and have devised a points system. Apart from checking out basics of Classcraft, I have not yet explored digital resources to support gamification. If any reader of this blog has some gamification strategies which they feel may work well in an RMT class, please contact me. I am all ears for this Great Stuff!
References
Hattie, J. (2012). Visible Learning for Teachers: maximizing impact on learning. London: Routledge.
Palincsar, A. S. (1984). Reciprocal teaching of comprehension-fostering and comprehension-monitoring activities. Cognition and Instruction, p. 59.
Polya, G. (1945). How To Solve It. New Jersey: Princeton University Press.
Queensland Curriculum and Assessment Authority. (2017). 21st century skills for senior curriculum: a position paper.
Queensland Curriculum and Assessment Authority. (2017). Specialist Mathematics 2019 v1.0: General Senior Syllabus. Brisbane: QCAA.
Yvonne Reilly, e. a. (2009). Reciprocal Teaching in Mathematics. MAV Conference 2009 (p. 8). Melbourne: The Mathematical Association of Victoria.
Leave a Reply